[Games101笔记]Lecture7~9 初学shading

最后修改于:2024年4月21日

Specular highlights

镜面高光

Diffuse reflection

漫反射

Ambient lighting

环境照明

物体表面的漫反射所呈现出的效果

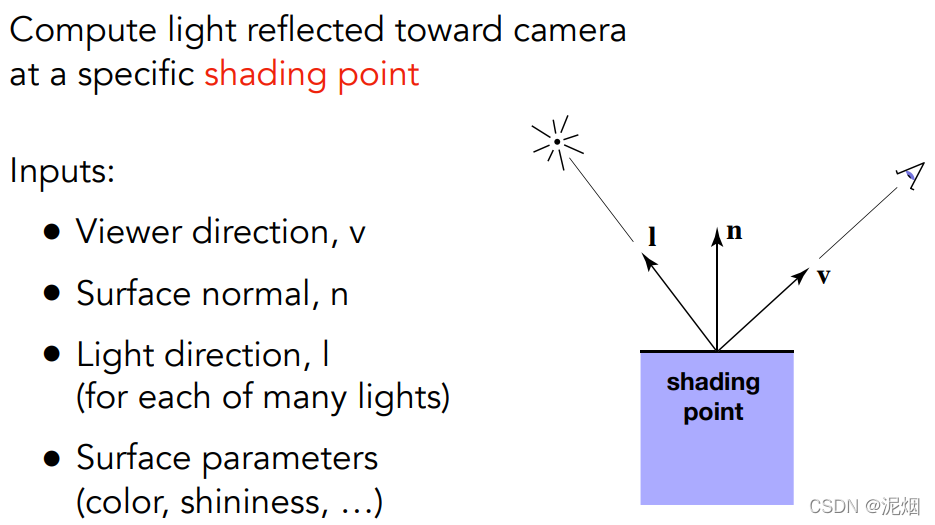
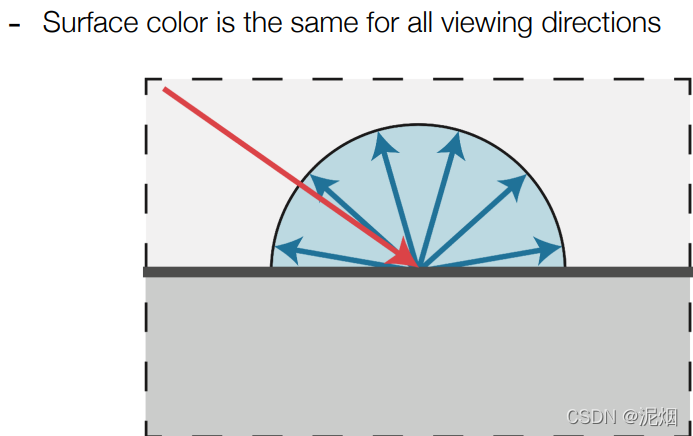
光通量看作不变的时候, 物体表面接收到的光线数量与角度有关

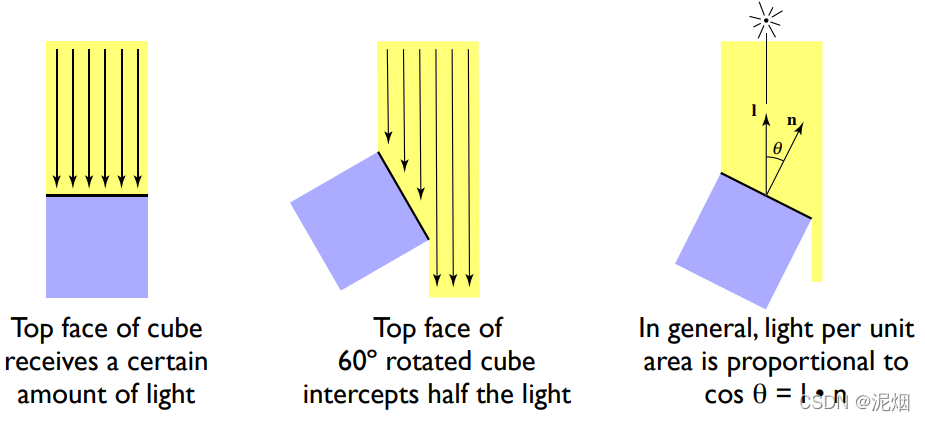
并且有能量守恒(远处能量衰减)

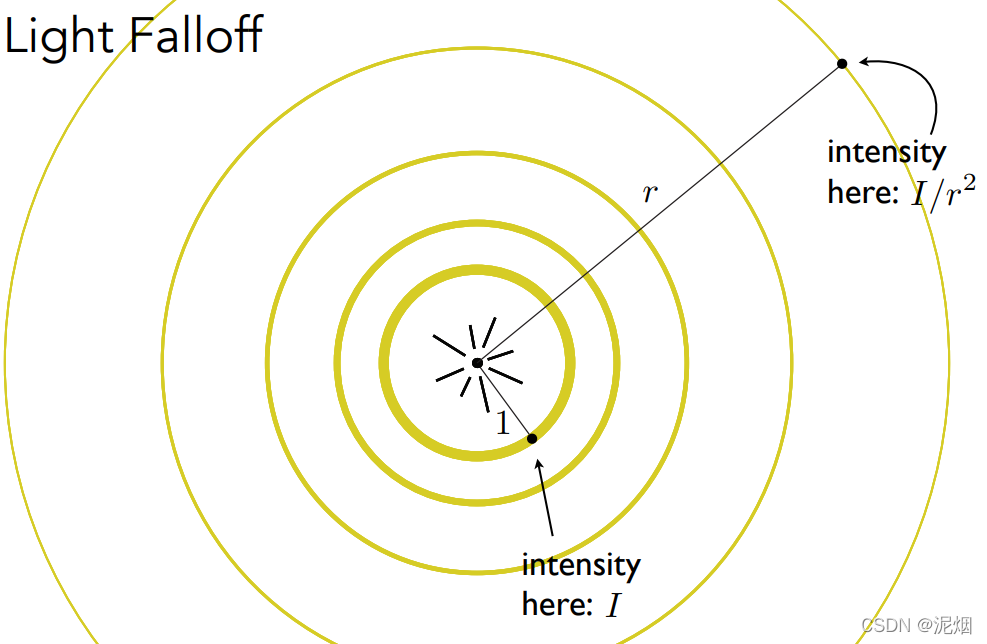
得出与视点方向无关的着色方式(n,l均为单位向量)

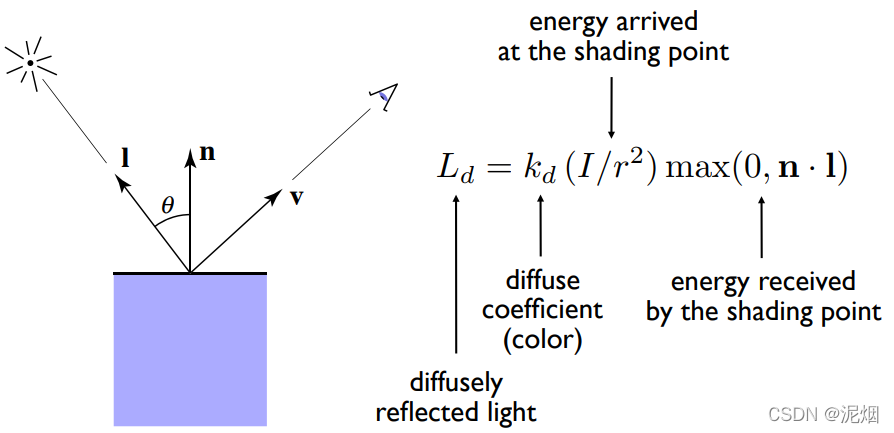
Kd为与漫反射有关的系数

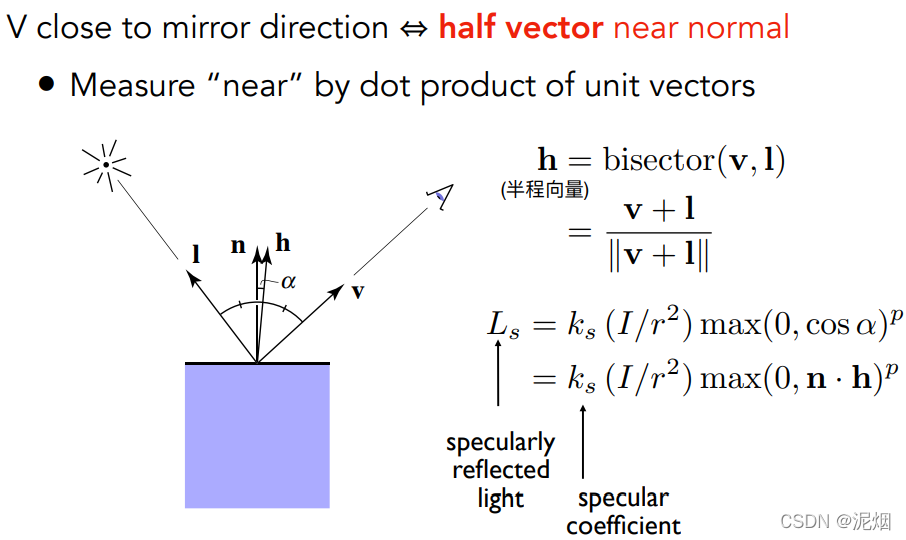
布林冯模型-经验模型,保证高光被看到

利用半程向量,有方便计算的作用

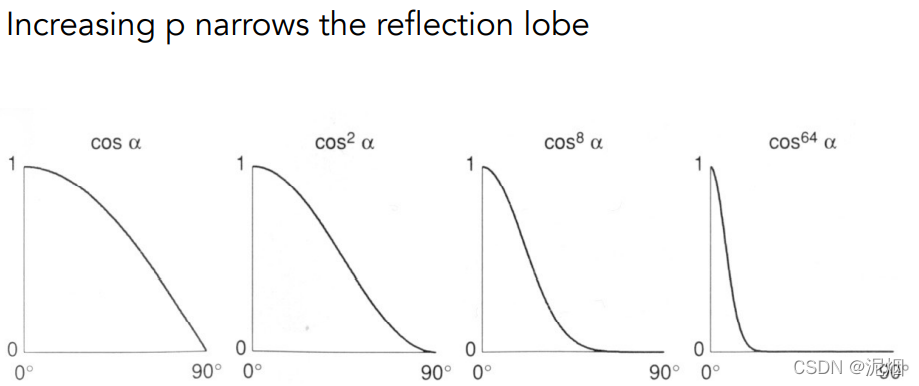
指数p,降低容忍度,更精确

求顶点法线的方法:

将顶点相邻的面法线加权求一个平均

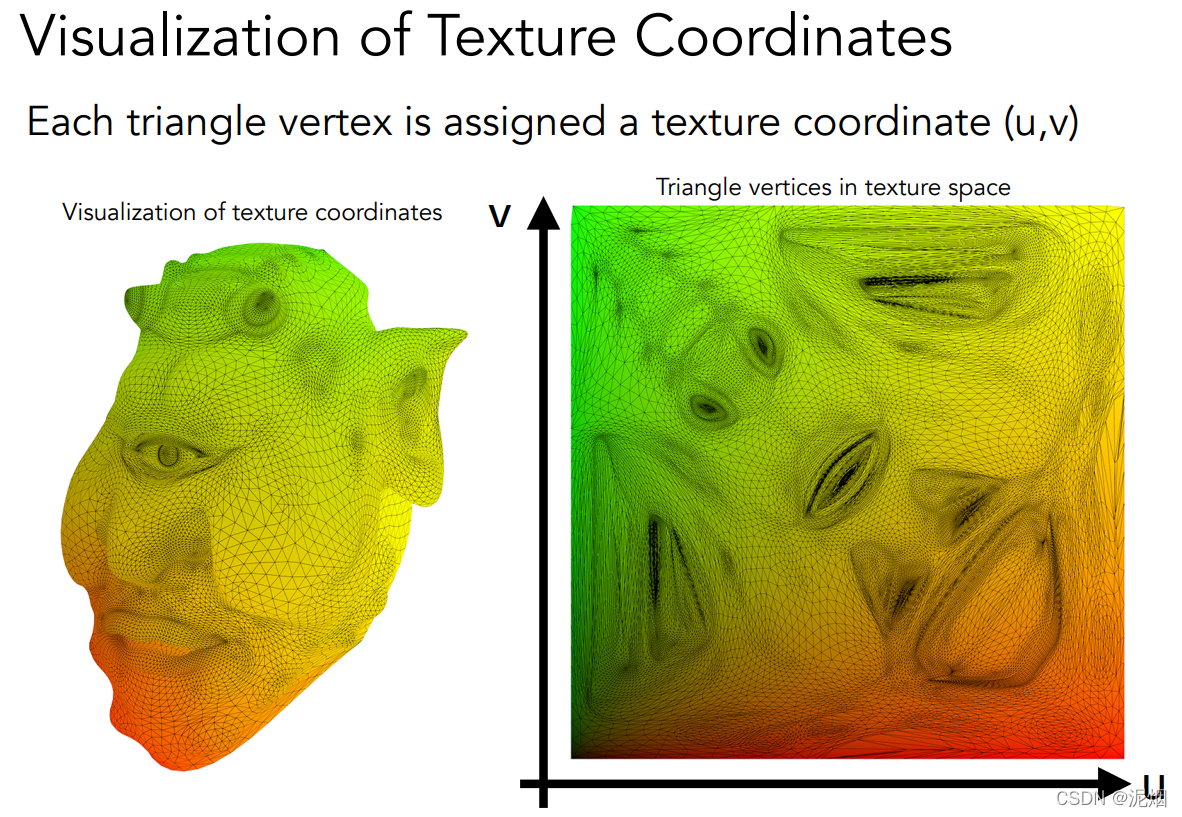
各个三角形的顶点对应一个u,v坐标 (约定俗成, 0≤u,v≤1)

对插值的理解

插值:三角形各顶点具有不同属性,如何使三角形内部的属性更加平滑得体现

若是想插值三维中的属性,需使用三维情况下的重心坐标,

(★注意:投影后,需要进行插值的点,其重心坐标基本都会改变)

双线性插值:所查询到的纹理坐标为非整数的情况

x可以看作是相似程度

效果对比

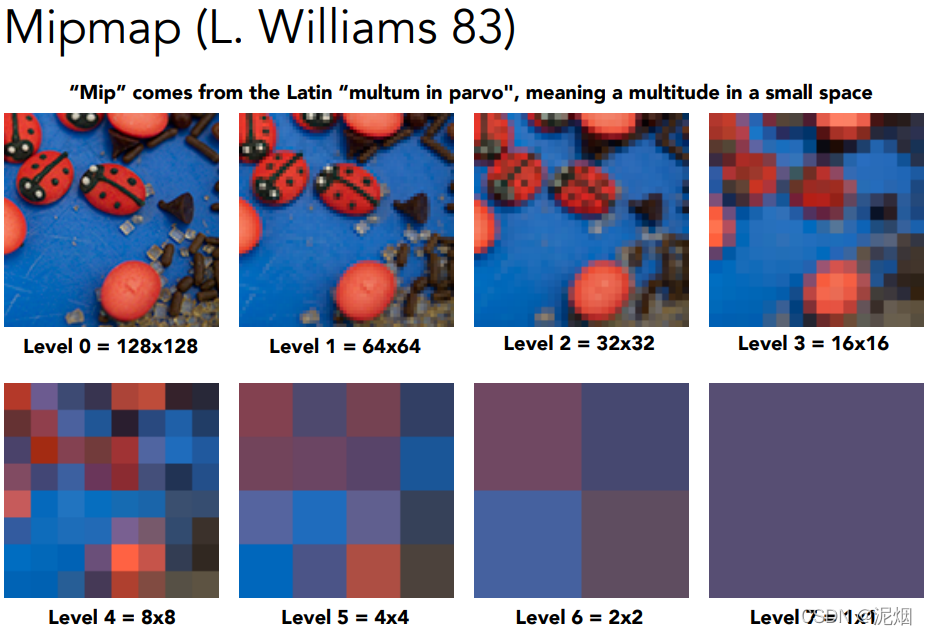
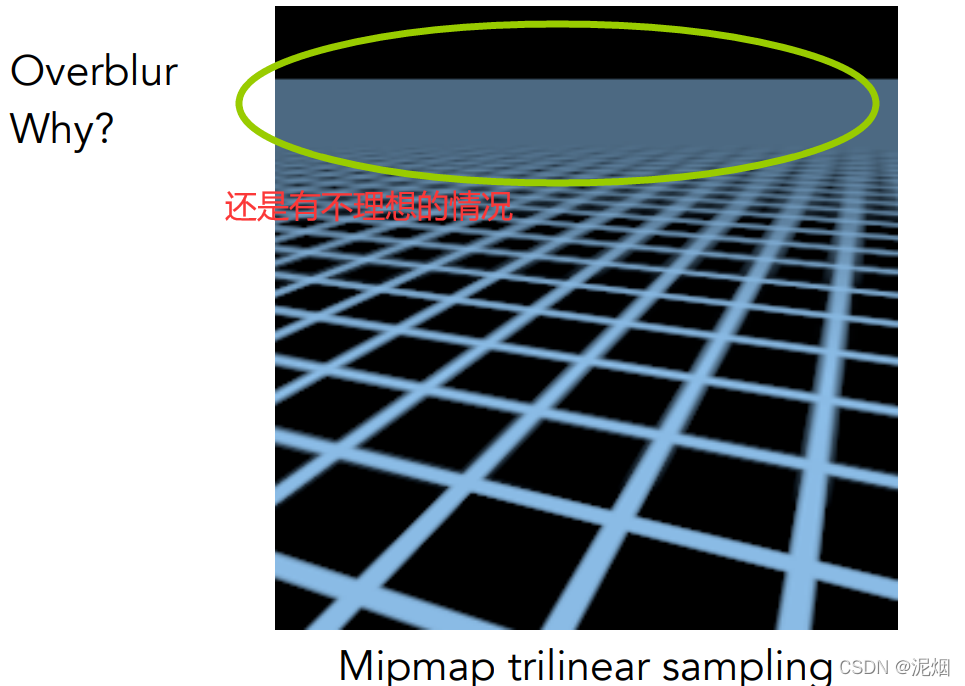
三线性插值:在维度上类似线性插值到双线性插值, 为了使过渡更自然, 利用Mipmap各层,实现非整数层的插值

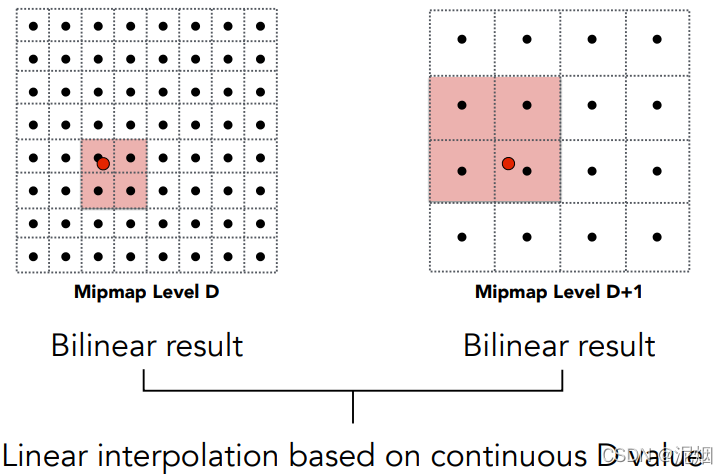
Mipmap:快,不准确,且适用于方形区域的范围查询

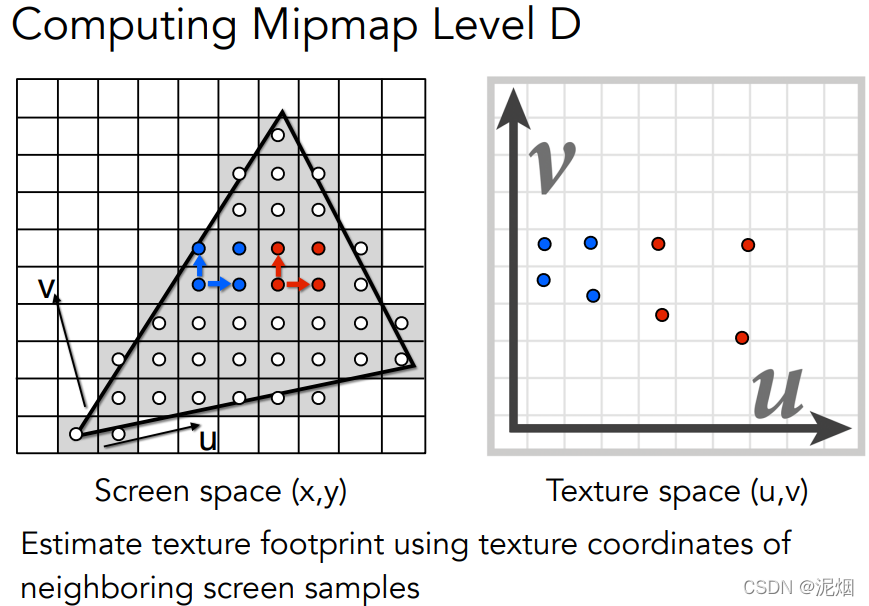
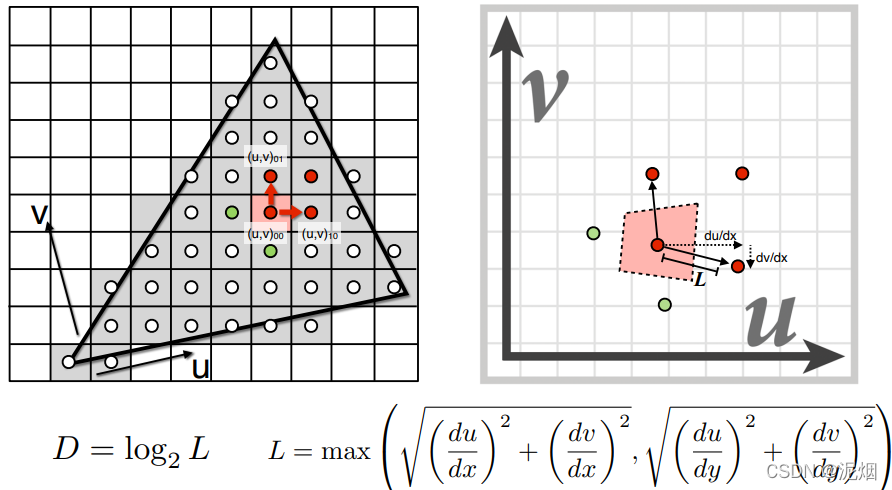
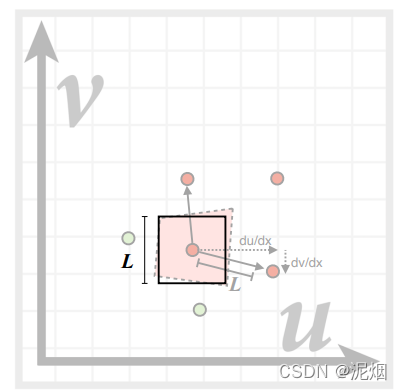
不同层级👇,这是三线性插值的方法中的关键

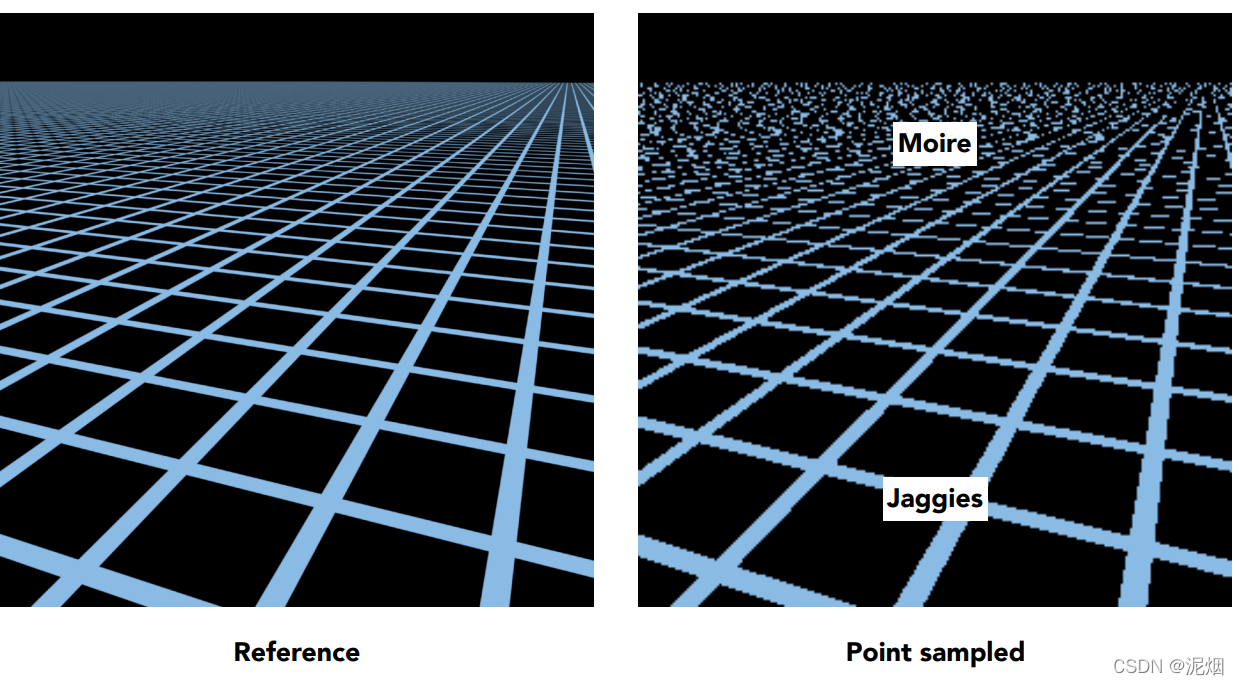
近处出现明显锯齿,远处则是摩尔纹

摩尔纹就是光栅化的算法导致的。

我们知道，一个三角形有顶点坐标和纹理坐标，纹理坐标范围是【0-1】。

光栅化的过程就是把三角形在屏幕上以一个个像素显示出来，插值计算三角形内部每个像素的顶点的数据，包括常见的深度与纹理坐标。

如果这个三角形距离camera近,也就是说在屏幕上占了较多的像素，那么相邻两个像素的纹理坐标是接近的，这样通过纹理坐标获得纹理贴图上的纹素值也是接近的，这样这俩个像素看起来就是较顺接流畅，视觉上不突兀，同时gpu读取也快速，因为大部分纹素读取是在cache中。

而如果这个三角形距离camera较远，也就是在屏幕上只占了很少的像素，这种情况就是一个小物体应用了一个大纹理，光栅化后，相邻两个像素的纹理坐标会差别好大，读出来的纹素也会差别很大，会很突兀，尤其是camera移动时特别难看，产生闪烁，火花现象，除此之外，gpu读取性能也很低效，因为两个相邻的像素所对应的纹素，一个可能在cache中，另一个还没有加载到cache中呢。而解决这种视觉和性能问题，mipmap就登场了

——摘自知乎网友的评论

纹理大所引发的问题:由于视图关系,最终着色后呈现在我们屏幕上的图像中,表示远处图像的一像素所代表的实际纹理是很多的,

而我们一味的利用周围像素当做插值的基本,会损失信息

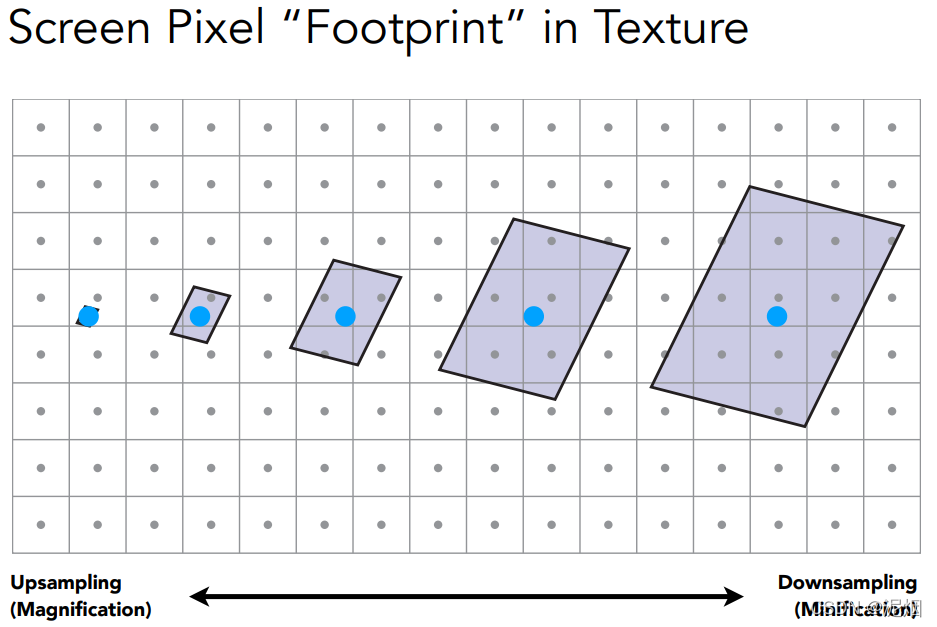
当然, 我们也可以把一个像素细分为更多个小的采样点, 即超采样,但计算量会很大

Mipmap的性质使其不适合用于不规则(非方形)的着色

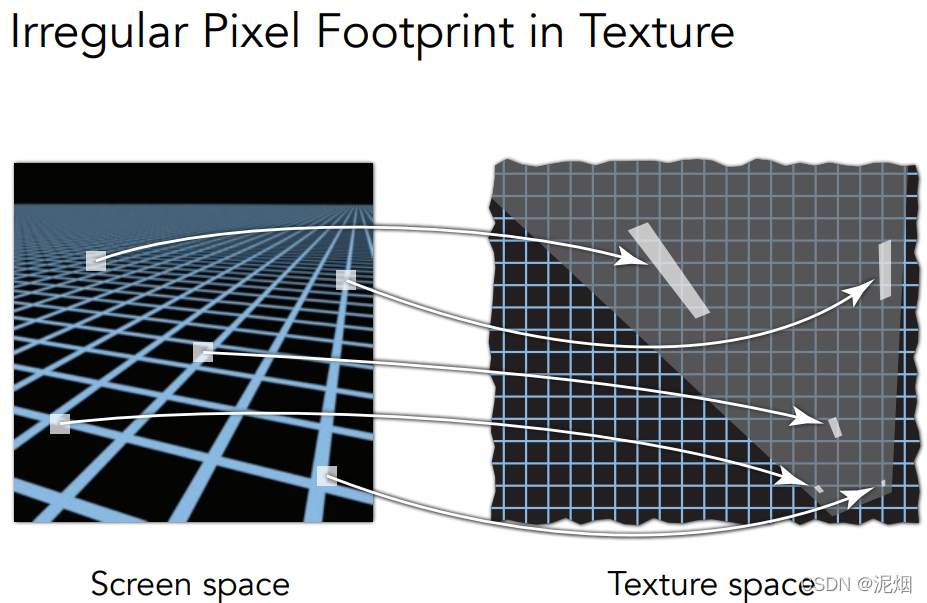
于是引用了各向异性的着色方法

效果更佳

总结

纹理过小产生的问题
造成原因：当纹理过小时，例如将一张200x200的纹理贴图应用在一600x600的屏幕上，必然会导致纹理走样失真，因为屏幕空间的几个像素点对应在纹理贴图的坐标上都是集中在一个像素大小之内，但是如果仅仅是使用坐标(u,v)在texture贴图下对应的最近的那个像素点，会造成更加严重的走样。
解决方案：使用双线性插值(Bilinear Interpolation)，即利用坐标(u,v)在texture贴图下水平及竖直方向对应最近的像素点偏移的比率来对纹理进行线性插值; 三线性插值是利用三次方程来进行两次插值，效果虽然可能更好，但是会耗费远高于双线性插值的算力资源，这并不是此次课题追求的性能与效果的平衡，故并没有采用。
纹理过大产生的问题
造成原因：屏幕空间的一个像素对应了纹理贴图上的一片范围的点，例如某个三角形面真正在纹理贴图上对应的一片区域有数十个像素点。但是由于透视的关系，距离很远的三角形面投影到近平面时可能只有几个像素点的大小(远远小于原来的像素大小)，假设这1个或2个像素采样texture的结果就要代表原来三角形面数十个像素点的颜色信息，从而形式上也就变成了一种欠采样。
解决方法：通过SuperSampling，即超采样，也就是当一个像素点的信息不足以代表一个区域的信息，那么便把该像素细分为更多个小的采样点，这种方法确实可以缓解走样现象，但是计算量太大了，当需要细分的图像很大或者随着屏幕空间离相机越来越远时，计算量会增大数千数万倍; 利用Mipmap技术可以用更小的计算量缓解欠采样，适用于正方形区域，在此思想上利用各向异性过滤的Mipmap适用于矩形区域，而不规则图形可用圆来分割，然后反复查询，即EWA过滤(也是一种Mipmap)