TRenderer
[toc]
环境(*:暂未使用)
-
cmake 3.29.2
-
GNU 9.2.0
-
*ninja 1.11.1(使用并行任务来编译工程)
-
assimp-5.2.5
-
Qt Creator 5.14.2
-
glm
-
*tbb(并行编程库)
记录:编译安装assimp并成功链接
参考资料:
在源码目录下
# 需修改路径
# cmake -G"MinGW Makefiles" -B build -DCMAKE_INSTALL_PREFIX=安装路径 -DWITH_SOME_OPTIONS=ON
cmake -G"MinGW Makefiles" -B build -DCMAKE_INSTALL_PREFIX=K:\code\QTProject\TRenderer\packages\assimp5.2.5 -DWITH_SOME_OPTIONS=ON
# 使用8个核并行编译
cmake --build build --parallel 8
cmake --build build --target install
但是还是链接不上.dll 动态库,
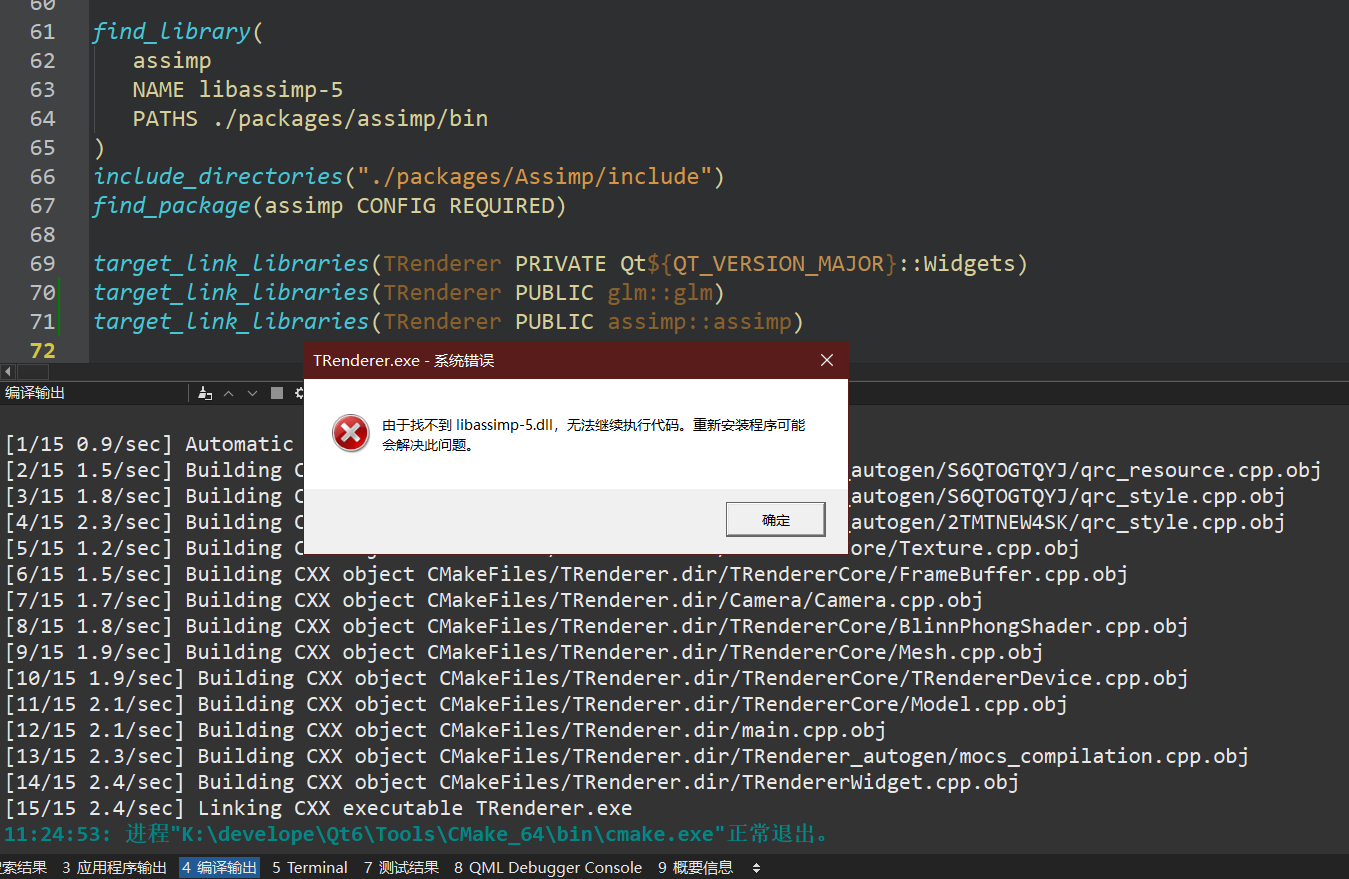
明明已经在CMakeList.txt中配置了
set(assimp_DIR ./packages/assimp5.2.5/lib/cmake/assimp-5.2)
find_package(assimp CONFIG REQUIRED)
target_link_libraries(TRenderer PUBLIC assimp::assimp)
相应的文件也是在这里(./packages/assimp5.2.5/lib/cmake/assimp-5.2)的,就是不知道为什么链接不上...
咨询群友过后, 发现把动态库libassimp-5.dll放在build好的目录下即可解决(.exe所在目录)

主要结构体/类/算法
BasicDataStruture

using Color = glm::vec3;
using Vector2D = glm::vec2;
using Vector3D = glm::vec3;
using VectorI3D = glm::ivec3;
using Vector4D = glm::vec4;
using VectorI4D = glm::ivec4;
using Coord2D = glm::vec2;
using CoordI2D = glm::ivec2;
using Coord3D = glm::vec3;
using CoordI3D = glm::ivec3;
using Coord4D = glm::vec4;
using CoordI4D = glm::ivec4;
using BorderPlane = glm::vec4;
using BorderLine = glm::vec3;
enum RenderMode{FACE,EDGE,VERTEX};
enum RenderColorType{BACKGROUND, LINE, POINT};
enum LightColorType{DIFFUSE, SPECULAR, AMBIENT};
struct Vertex
{
Coord3D worldSpacePos;
union
{
Coord4D clipSpacePos;
Coord4D ndcSpacePos;
};
CoordI2D screenPos;
float screenDepth;
Vector3D normal;
Coord2D texCoord;
};
using Triangle = std::array<Vertex, 3>;
using Line = std::array<CoordI2D, 2>;
struct Fragment
{
Coord3D worldSpacePos;
CoordI2D screenPos;
float screenDepth;
Color fragmentColor;
Vector3D normal;
Coord2D texCoord;
};
struct Light
{
union{
Coord4D pos;
Vector4D dir;
};
Color ambient;
Color diffuse;
Color specular;
};
struct Material
{
int diffuse;
int specular;
float shininess;
};
+struct Vertex {
-Coord3D worldSpacePos // 世界空间位置
-union {
-Coord4D clipSpacePos // 裁剪空间位置
-Coord4D ndcSpacePos // 归一化设备坐标空间位置
}
-CoordI2D screenPos // 屏幕位置
-float screenDepth // 屏幕深度
-Vector3D normal // 法向量
-Coord2D texCoord // 纹理坐标
}
+struct Fragment {
-Coord3D worldSpacePos // 世界空间位置
-CoordI2D screenPos // 屏幕位置
-float screenDepth // 屏幕深度
-Color fragmentColor // 片元颜色
-Vector3D normal // 法向量
-Coord2D texCoord // 纹理坐标
}
+struct Light {
-union {
-Coord4D pos // 位置
-Vector4D dir // 方向
}
-Color ambient // 环境光颜色
-Color diffuse // 漫反射颜色
-Color specular // 镜面反射颜色
}
+struct Material {
-int diffuse // 漫反射
-int specular // 镜面反射
-float shininess // 高光度
}
EdgeEquation

计算边缘方程的参数
图形学底层探秘 - 更现代的三角形光栅化与插值算法的实现与优化 - 知乎 (zhihu.com)
EdgeEquation::EdgeEquation(const Triangle &tri)
{
I = {
tri[0].screenPos.y - tri[1].screenPos.y,
tri[1].screenPos.y - tri[2].screenPos.y,
tri[2].screenPos.y - tri[0].screenPos.y};
J = {
tri[1].screenPos.x - tri[0].screenPos.x,
tri[2].screenPos.x - tri[1].screenPos.x,
tri[0].screenPos.x - tri[2].screenPos.x};
K = {
tri[0].screenPos.x * tri[1].screenPos.y - tri[0].screenPos.y * tri[1].screenPos.x,
tri[1].screenPos.x * tri[2].screenPos.y - tri[1].screenPos.y * tri[2].screenPos.x,
tri[2].screenPos.x * tri[0].screenPos.y - tri[2].screenPos.y * tri[0].screenPos.x};
topLeftFlag[0] = JudgeOnTopLeftEdge(tri[0].screenPos,tri[1].screenPos);
topLeftFlag[1] = JudgeOnTopLeftEdge(tri[1].screenPos,tri[2].screenPos);
topLeftFlag[2] = JudgeOnTopLeftEdge(tri[2].screenPos,tri[0].screenPos);
twoArea = K[0] + K[1] + K[2];
delta = 1.f / twoArea;
}
EdgeEquation的构造函数,通过三角形的屏幕空间坐标计算边缘方程的参数,在构造函数中进行了初始化设置,为后续的三角形光栅化处理提供了基础的边缘方程计算和判断。
计算边缘方程的参数:
首先计算了三条边的斜率参数 I 和 J,以及常数项 K。这些参数用于后续的边缘方程计算。
- I、J、K 的计算基于三角形的三个顶点的屏幕空间坐标,利用差分计算两个点的坐标差。
topLeftFlag数组用于存储判断三角形的每条边是否在屏幕上部左侧的标志,这个标志在判断像素是否在三角形内部时会用到。twoArea是三角形的两倍面积,用于面剔除判断和像素插值计算。
delta是计算插值时使用的参数,它是1 / twoArea。代码中的
JudgeOnTopLeftEdge函数用于判断某个点是否在另外两个点的上部或者左侧,这是判断三角形边缘在屏幕上部左侧的标志。
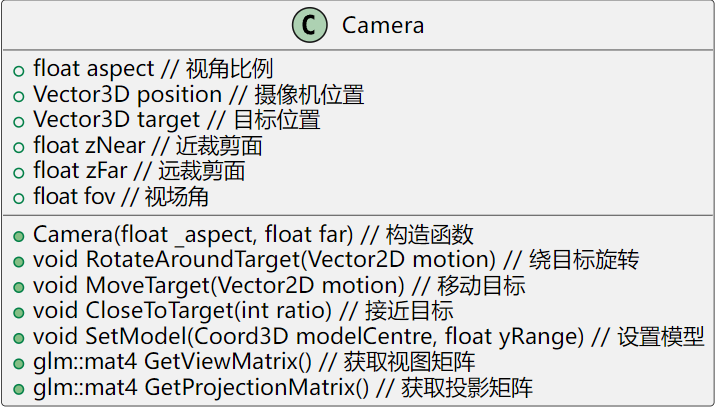
Camera
Shader

BlinnPhongShader

FragmentShader
FrameBuffer

Mesh

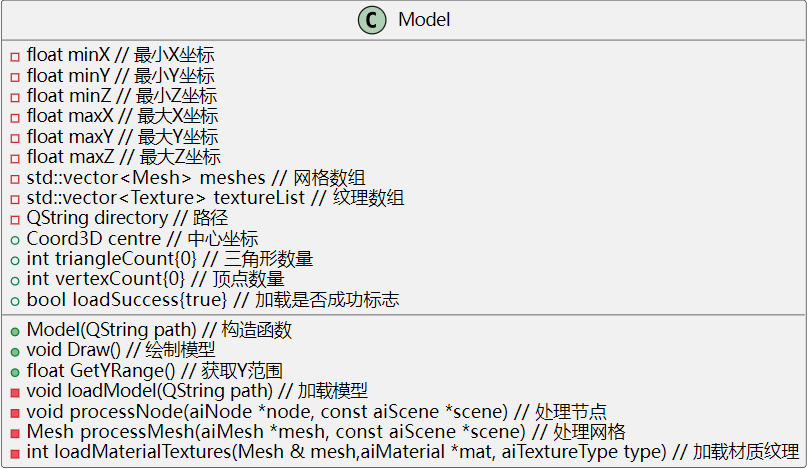
Model
Texture

TRendererDevice
TRendererDevice(int w, int h);
TRendererDevice(const TRendererDevice&) = delete;
TRendererDevice(TRendererDevice &&) = delete;
TRendererDevice& operator=(const TRendererDevice&) = delete;
TRendererDevice& operator=(TRendererDevice&&) = delete
是在 TRendererDevice 类中定义特殊的成员函数,用于控制对象的拷贝和移动操作。
-
TRendererDevice(int w, int h);:这是类的构造函数,用于创建TRendererDevice对象。它接受两个参数w和h,分别表示宽度和高度。 -
TRendererDevice(const TRendererDevice&) = delete;:这是删除拷贝构造函数的语法。通过将拷贝构造函数标记为删除,表明禁止使用拷贝构造函数来创建新对象,即不允许通过拷贝构造函数进行对象的复制。 -
TRendererDevice(TRendererDevice &&) = delete;:这是删除移动构造函数的语法。同样地,通过将移动构造函数标记为删除,表明禁止使用移动构造函数来创建新对象,即不允许通过移动构造函数进行对象的移动构造。 -
TRendererDevice& operator=(const TRendererDevice&) = delete;:这是删除拷贝赋值运算符的语法。通过将拷贝赋值运算符标记为删除,表明禁止使用拷贝赋值运算符来进行对象的赋值操作,即不允许通过拷贝赋值运算符来将一个对象的值复制给另一个对象。 -
TRendererDevice& operator=(TRendererDevice&&) = delete;:这是删除移动赋值运算符的语法。同样地,通过将移动赋值运算符标记为删除,表明禁止使用移动赋值运算符来进行对象的移动赋值操作,即不允许通过移动赋值运算符来将一个对象的值移动给另一个对象。
这些删除操作符的作用是为了防止对象的拷贝和移动,从而保证类的对象在程序中不会被意外地复制或移动,确保代码的稳定性和安全性。通常情况下,如果某个类的对象不需要被拷贝或移动,就可以将对应的拷贝构造函数、移动构造函数、拷贝赋值运算符和移动赋值运算符标记为删除。
Half-Space 三角形光栅化算法
(PDF) Accelerated Half-Space Triangle Rasterization (researchgate.net)
// Half-Space 三角形光栅化算法
void TRendererDevice::RasterizationTriangle(Triangle &tri)
{
CoordI4D boundingBox = GetBoundingBox(tri);
int xMin = boundingBox[0];
int yMin = boundingBox[1];
int xMax = boundingBox[2];
int yMax = boundingBox[3];
EdgeEquation triEdge(tri);
if(faceCulling && triEdge.twoArea <= 0) return;
else if(triEdge.twoArea == 0) return;
Fragment frag;
VectorI3D cy = triEdge.GetResult(xMin, yMin);
for(int y = yMin; y <= yMax; y++)
{
VectorI3D cx = cy;
for(int x = xMin; x <= xMax; x++)
{
if(JudgeInsideTriangle(triEdge, cx))
{
Vector3D barycentric = triEdge.GetBarycentric(cx);
float screenDepth = CalculateInterpolation(tri[0].screenDepth, tri[1].screenDepth, tri[2].screenDepth, barycentric);
if (frameBuffer.JudgeDepth(x, y, screenDepth))
{
float viewDepth = 1.0f / (barycentric.x / tri[0].ndcSpacePos.w + barycentric.y / tri[1].ndcSpacePos.w + barycentric.z / tri[2].ndcSpacePos.w);
frag = ConstructFragment(x, y, screenDepth, viewDepth, tri, barycentric);
shader->FragmentShader(frag);
frameBuffer.SetPixel(frag.screenPos.x,frag.screenPos.y,frag.fragmentColor);
}
}
triEdge.UpX(cx);
}
triEdge.UpY(cy);
}
}
半空间三角形栅格化算法,即对三角形进行像素化处理以便在屏幕上进行渲染。
主要步骤如下:
- 获取三角形的包围盒:
首先调用
GetBoundingBox(tri)获取三角形的包围盒,得到包围盒的最小和最大的 x、y 坐标。创建边缘方程对象:
使用
EdgeEquation triEdge(tri)创建一个边缘方程对象,该对象用于后续判断像素是否在三角形内部。面剔除判断:
- 如果启用了面剔除(
faceCulling为真),并且三角形的两倍面积小于等于 0,则直接返回,不进行后续的像素处理。否则,如果三角形的两倍面积等于 0,也直接返回,因为这种情况下三角形是退化的,不需要进行像素处理。
逐像素处理:
- 从包围盒的最小 x、y 坐标开始,遍历包围盒内的每个像素。
- 对于每个像素,通过边缘方程判断其是否在三角形内部(调用
JudgeInsideTriangle(triEdge, cx))。- 如果在三角形内部,则计算其重心坐标(barycentric)和屏幕深度(screenDepth),并根据重心坐标插值计算视图空间深度(viewDepth)。
- 利用计算得到的像素信息,构造一个片元对象(
frag = ConstructFragment(x, y, screenDepth, viewDepth, tri, barycentric)),然后调用着色器的片元着色器方法shader->FragmentShader(frag)进行光照计算,最后将计算得到的颜色值设置到帧缓冲区的对应像素位置上。总体来说,这段代码是对三角形进行光栅化处理的核心部分,通过边缘方程判断像素是否在三角形内部,然后进行像素插值计算深度和颜色,最终将计算得到的颜色值渲染到帧缓冲区中。
Bresenham 画线算法
// Bresenham 画线算法
void TRendererDevice::DrawLine(Line& line)
{
// 将线段的起点和终点坐标转换为整数,并且限制在屏幕范围内
int x0 = glm::clamp(static_cast<int>(line[0].x), 0, w - 1);
int x1 = glm::clamp(static_cast<int>(line[1].x), 0, w - 1);
int y0 = glm::clamp(static_cast<int>(line[0].y), 0, h - 1);
int y1 = glm::clamp(static_cast<int>(line[1].y), 0, h - 1);
bool steep = false;
// 如果线段在x方向上的变化量小于y方向上的变化量,则将x和y互换,标记为steep
if (abs(x0 - x1) < abs(y0 - y1))
{
std::swap(x0, y0);
std::swap(x1, y1);
steep = true;
}
// 如果起点x坐标大于终点x坐标,则交换起点和终点的x和y坐标
if (x0 > x1)
{
std::swap(x0, x1);
std::swap(y0, y1);
}
int dx = x1 - x0;
int dy = y1 - y0;
int k = dy > 0 ? 1 : -1; // 判断y方向上的变化方向
if (dy < 0)dy = -dy;
float e = -dx; // 计算误差值
int x = x0, y = y0;
while (x != x1)
{
if (steep)frameBuffer.SetPixel(y, x, lineColor);
else frameBuffer.SetPixel(x, y, lineColor);
e += (2 * dy); // 更新误差值
if (e > 0)
{
y += k;
e -= (2 * dx);
}
++x; // 移动到下一个像素点
}
}
高级计算机图形学 中科大课件 光栅化 Bresenham画线算法
Bresenham快速画直线算法 - 冷夜 - 网游编程技术 - 博客园 (cnblogs.com)
Deepnight Games | Bresenham algorithm
Bresenham 线绘制算法 | 他山教程,只选择最优质的自学材料 (tastones.com)
Bresenham 直线算法是一种用于绘制直线的经典算法,它能够高效地计算出直线上的各个像素点,适用于计算机图形学中的线段绘制和光栅化。
主要针对整数坐标系下的直线绘制,核心思想是通过计算直线斜率的变化,利用误差项来控制像素点的绘制位置,从而实现直线的连续绘制。Bresenham 直线算法的基本步骤:
对于给定的直线起点 (x0, y0) 和终点 (x1, y1),计算直线斜率的绝对值 |m|,其中 m = (y1 - y0) / (x1 - x0)。
根据直线的斜率 |m| 的大小,分为两种情况处理:
- 当 |m| <= 1 时,直线的倾斜程度较小,在 x 方向上步进;
当 |m| > 1 时,直线的倾斜程度较大,在 y 方向上步进。
根据斜率的不同,选择适当的步进方式,并计算误差项 e 的初始值。
进入主循环,根据步进方式逐个计算并绘制像素点,同时更新误差项 e:
- 当斜率 |m| <= 1 时,每次步进 x 方向一个像素,误差项 e 的更新公式为 e += 2dy - 2dx,其中 dx 表示 x 方向的步进,dy 表示 y 方向的步进。
当斜率 |m| > 1 时,每次步进 y 方向一个像素,误差项 e 的更新公式为 e += 2dx - 2dy。
在每次更新误差项 e 后,判断 e 是否超过阈值(通常为 dx 或 dy 的一半),若超过阈值,则向 x 或 y 方向步进一个像素,并调整误差项 e。
循环直到绘制完成,即直线的终点坐标达到目标值。
Cohen-Sutherland & Sutherland-Hodgman 算法(齐次空间裁剪)
// Cohen-Sutherland算法(线段裁剪)
std::optional<Line> TRendererDevice::ClipLine(Line& line)
{
// 计算线段端点的裁剪码
std::bitset<4> code[2] =
{
GetClipCode(Coord3D(line[0], 1), screenLines),
GetClipCode(Coord3D(line[1], 1), screenLines)
};
// 如果两个端点都在裁剪区域内,则直接返回
if((code[0] | code[1]).none()) return line;
// 如果两个端点都在裁剪区域外,则直接丢弃该直线
if((code[0] & code[1]).any()) return std::nullopt;
for(int i = 0; i < 4; i++)
{
// 如果两个端点在不同的裁剪区域内部或外部
// 裁剪码是通过位编码来表示点的位置关系的
// 对两个裁剪码进行位异或运算,取索引为i的位,可检查两端点在第i位上是否不同
if((code[0] ^ code[1])[i])
{
// 计算直线端点到裁剪平面的距离
float da = CalculateDistance(Coord3D(line[0], 1), screenLines[i]);
float db = CalculateDistance(Coord3D(line[1], 1), screenLines[i]);
// 计算交点处的插值系数
float alpha = da / (da - db);
// 计算交点的屏幕坐标
CoordI2D np = CalculateInterpolation(line[0], line[1], alpha);
// 根据裁剪平面的不同,更新直线的端点和裁剪码
if(da > 0){
line[1] = np;
code[1] = GetClipCode(Coord3D(np, 1), screenLines);
}else{
line[0] = np;
code[0] = GetClipCode(Coord3D(np, 1), screenLines);
}
}
}
return line;
}
// Sutherland-Hodgman 算法(齐次空间裁剪)
std::vector<Triangle> TRendererDevice::ClipTriangle(Triangle &tri)
{
// 计算三角形三个顶点的裁剪码
std::bitset<6> code[3] =
{
GetClipCode(tri[0].clipSpacePos, viewPlanes),
GetClipCode(tri[1].clipSpacePos, viewPlanes),
GetClipCode(tri[2].clipSpacePos, viewPlanes)
};
// 如果三个顶点的裁剪码均为0,即三角形完全在视锥体内,无需裁剪,直接返回原始三角形
// 如果三个顶点的裁剪码的与运算结果为非0,即三角形完全在视锥体外部,丢弃该三角形
if((code[0] | code[1] | code[2]).none())
return {tri};
if((code[0] & code[1] & code[2]).any())
return {};
// 检查三角形是否与近裁剪平面相交
if(((code[0] ^ code[1])[0]) || ((code[1] ^ code[2])[0]) || ((code[2] ^ code[0])[0]))
{
std::vector<Vertex> res;
// 遍历三个边,对与近裁剪平面相交的边进行裁剪
for(int i = 0; i < 3; i++)
{
int k = (i + 1) % 3;
if(!code[i][0] && !code[k][0]) // 边完全在内部
{
res.push_back(tri[k]);
}
else if(!code[i][0] && code[k][0]) // 边与近裁剪平面相交
{
float da = CalculateDistance(tri[i].clipSpacePos, viewPlanes[0]);
float db = CalculateDistance(tri[k].clipSpacePos, viewPlanes[0]);
float alpha = da / (da - db);
Vertex np = CalculateInterpolation(tri[i], tri[k], alpha);
res.push_back(np);
}
else if(code[i][0] && !code[k][0]) // 边与近裁剪平面相交
{
float da = CalculateDistance(tri[i].clipSpacePos, viewPlanes[0]);
float db = CalculateDistance(tri[k].clipSpacePos, viewPlanes[0]);
float alpha = da / (da - db);
Vertex np = CalculateInterpolation(tri[i], tri[k], alpha);
res.push_back(np);
res.push_back(tri[k]);
}
}
// 返回裁剪后的三角形
return ConstructTriangle(res);
}
return std::vector<Triangle>{tri};
}
Cohen-Sutherland算法和Sutherland-Hodgman算法都是常见的线段裁剪算法,用于对线段或多边形进行裁剪操作,特别是在计算机图形学中应用广泛。它们基于不同的思想和处理方式,分别适用于线段和多边形的裁剪,可以有效地提高渲染效率和图形显示效果。
Cohen-Sutherland算法(线段裁剪)
- 思想:
- Cohen-Sutherland算法采用线段与视口边界的裁剪码比较的思想,将视口划分为9个区域,每个区域对应一个裁剪码,表示线段相对于视口边界的位置关系。
通过比较线段两端点的裁剪码,可以确定线段与视口边界的相交情况,并进行裁剪操作。
步骤:
- 计算线段两端点的裁剪码,并进行位运算比较。
- 根据裁剪码的组合情况,确定线段与视口边界的位置关系,进行裁剪处理。
- 如果线段完全在视口内,则保留线段;如果线段完全在视口外,则舍弃;如果线段部分在视口内部,则对线段进行裁剪。
Sutherland-Hodgman算法(多边形裁剪)
思想:
Sutherland-Hodgman算法主要用于对多边形进行裁剪操作,它采用多边形顶点的位置关系和裁剪边的位置关系来确定裁剪结果。
算法基于逐顶点的迭代处理,通过对多边形的每个顶点进行裁剪,逐步得到裁剪后的多边形。
步骤:
- 对多边形的每条边进行检查,判断边是否与裁剪边界相交。
- 如果边完全在裁剪边界内,则保留整条边。
- 如果边与裁剪边界相交,则计算交点,将交点添加到裁剪后的多边形顶点列表中。
- 最后根据裁剪后的顶点列表重新构建裁剪后的多边形。
齐次空间裁剪是对三维空间中的物体进行裁剪的一种方法,与传统的Cohen-Sutherland算法(主要用于二维直线裁剪)有所不同
Sutherland–Hodgman 算法介绍(简单易懂)_sutherland-hodgman-CSDN博客
Polygon Clipping | Sutherland–Hodgman Algorithm - GeeksforGeeks
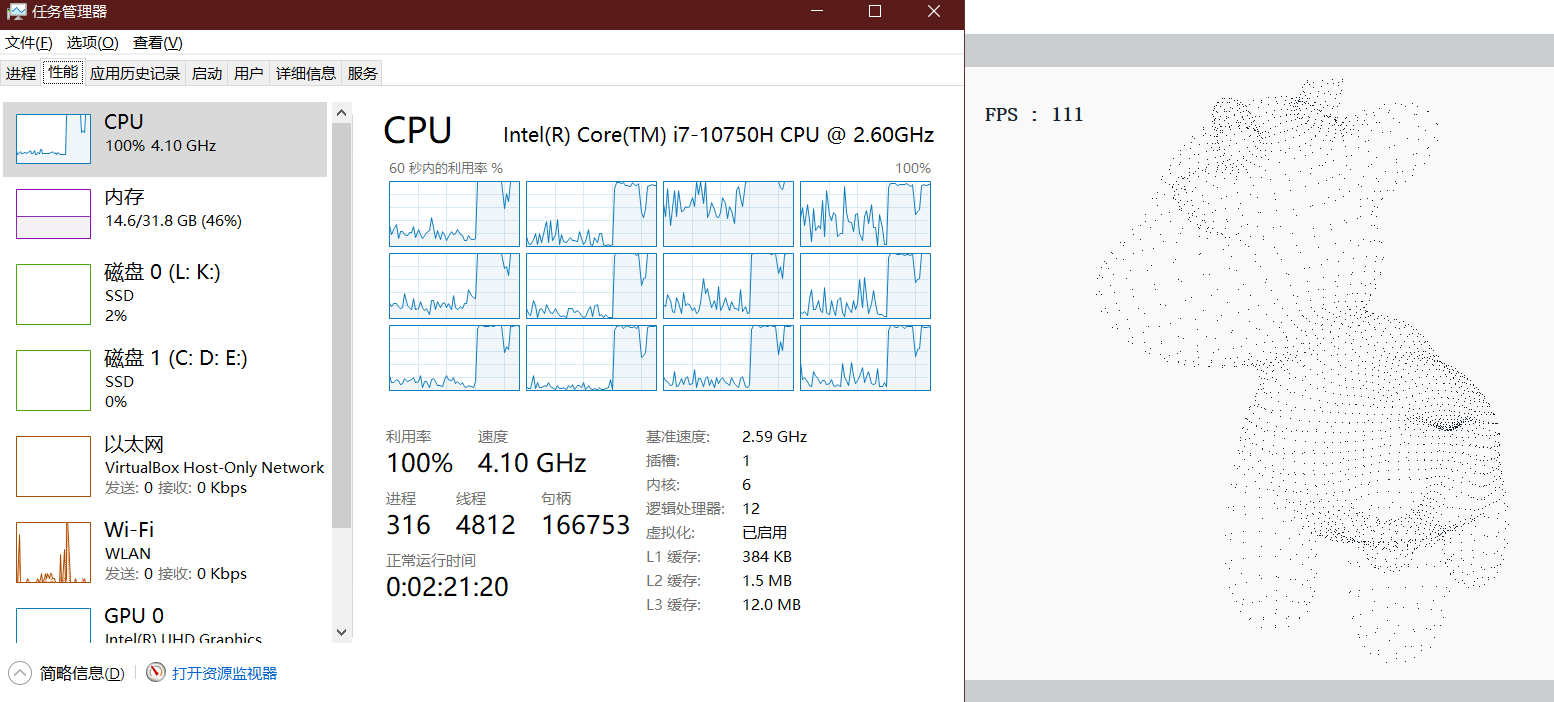
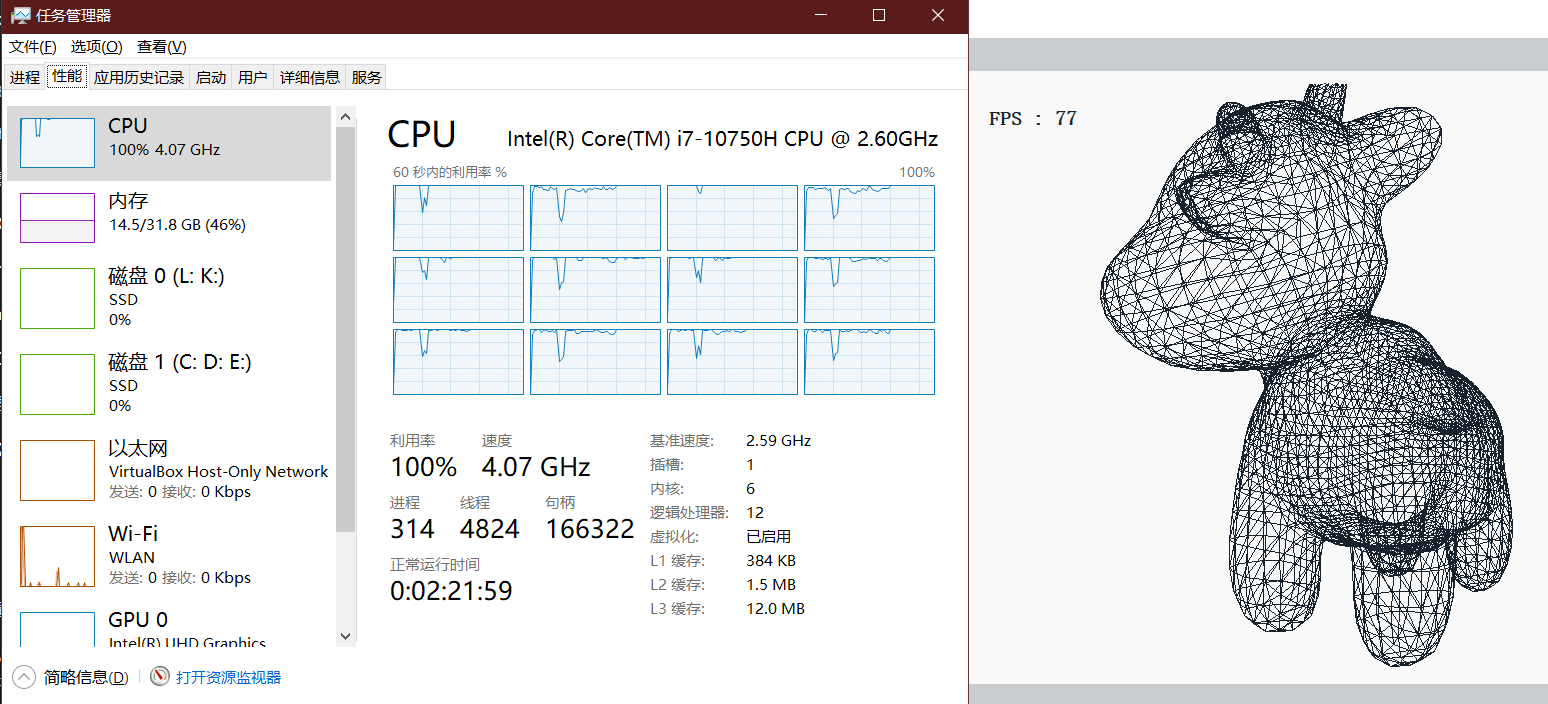
尝试使用多线程优化
不开多线程时
我的电脑cpu规格: NVIDIA GeForce GTX 1650 Ti Mobile Specs | TechPowerUp GPU Database
(顶点)

(顶点三角形)
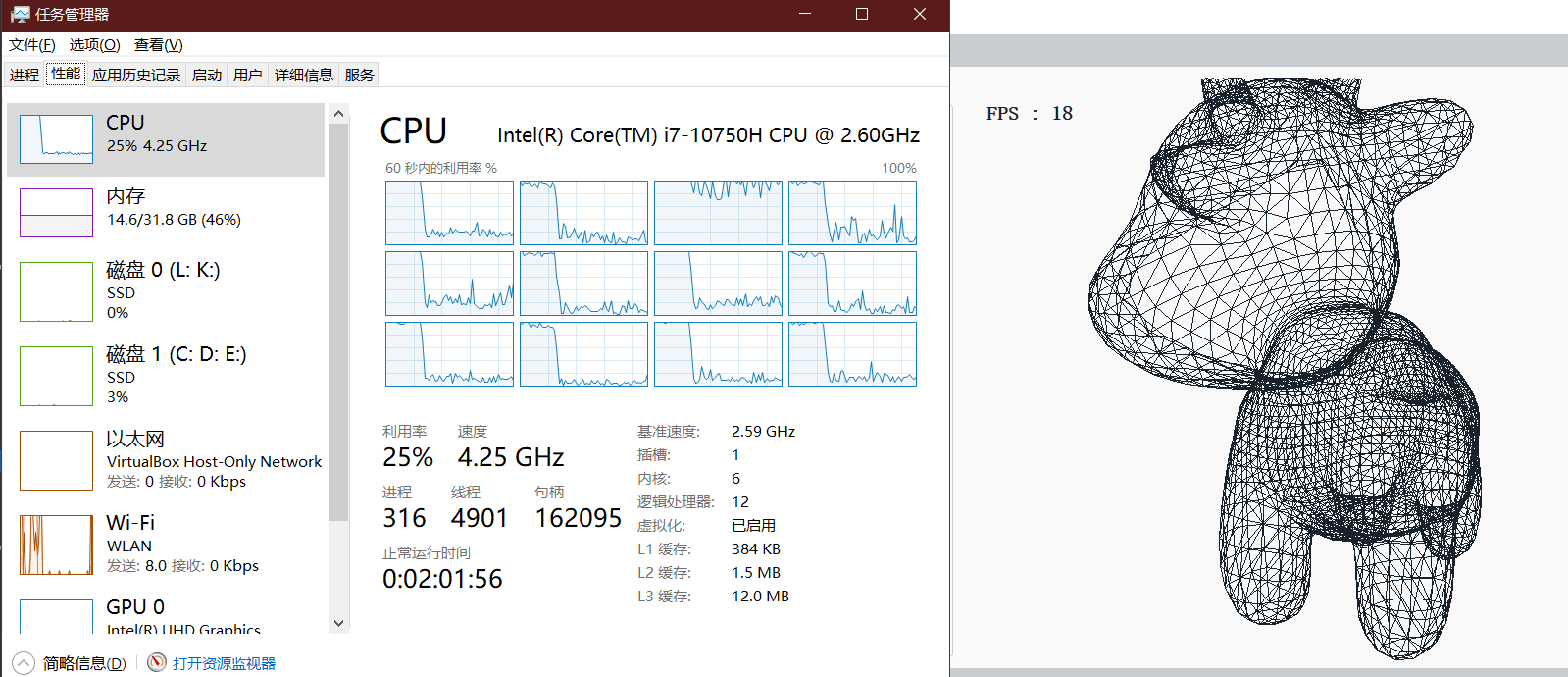
(渲染)
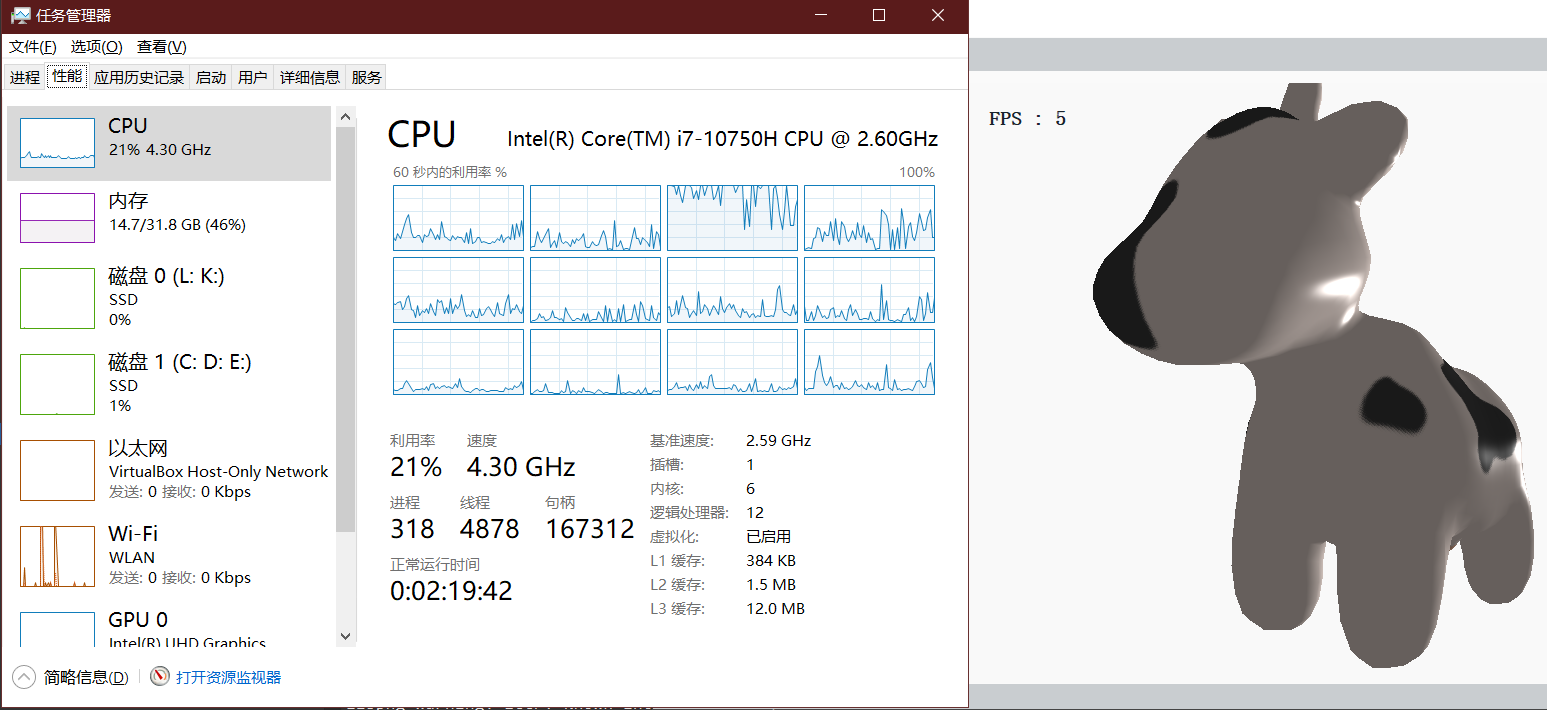
🆚对比:TBB, openglMP, c++11原生多线程
| Library | Provider | Implementation Approach | Affinity | Affinity Setup Method |
|---|---|---|---|---|
| OpenMP 4.0 | Intel | parallel for pragma with reduction clause | threads pinned to cores | KMP_AFFINITY environment variable |
| TBB 4.4 | Intel | parallel_reduce functor | threads pinned to cores | affinity_partitioner and custom task_scheduler_observer |
| C++11 Threads | GNU (libstdc++, GCC 4.8) | thread pool with task queue, return via future | threads pinned to cores | pthreads API |
Benchmarks: Threading - OpenMP vs TBB vs C++11 | Xcelerit
C++并行编程探讨分析(OpenMP & TBB & Thread Pool) - 小金乌会发光-Z&M - 博客园 (cnblogs.com)
oneTBB(尚未解决与QT发生的冲突)
CMakeLists.txt
set(TBB_DIR ./packages/oneapi-tbb-2021.1.1/lib/cmake/tbb)
find_package(TBB CONFIG REQUIRED)
target_link_libraries(TRenderer PUBLIC TBB::tbb)
tbb::parallel_for(tbb::blocked_range<size_t>(0, triangleList.size()),
[&](tbb::blocked_range<size_t> r)
{
for(size_t i = r.begin(); i < r.end(); i++)
ProcessTriangle(triangleList[i]);
});

profiling.h conflicts with Qt · Issue #547 · oneapi-src/oneTBB (github.com)
C++11 的thread库
std::vector<std::thread> threads;
for (size_t i = 0; i < triangleList.size(); i++) {
threads.emplace_back([&](size_t idx) {
ProcessTriangle(triangleList[idx]);
}, i);
}
for (auto& thread : threads) {
thread.join();
}
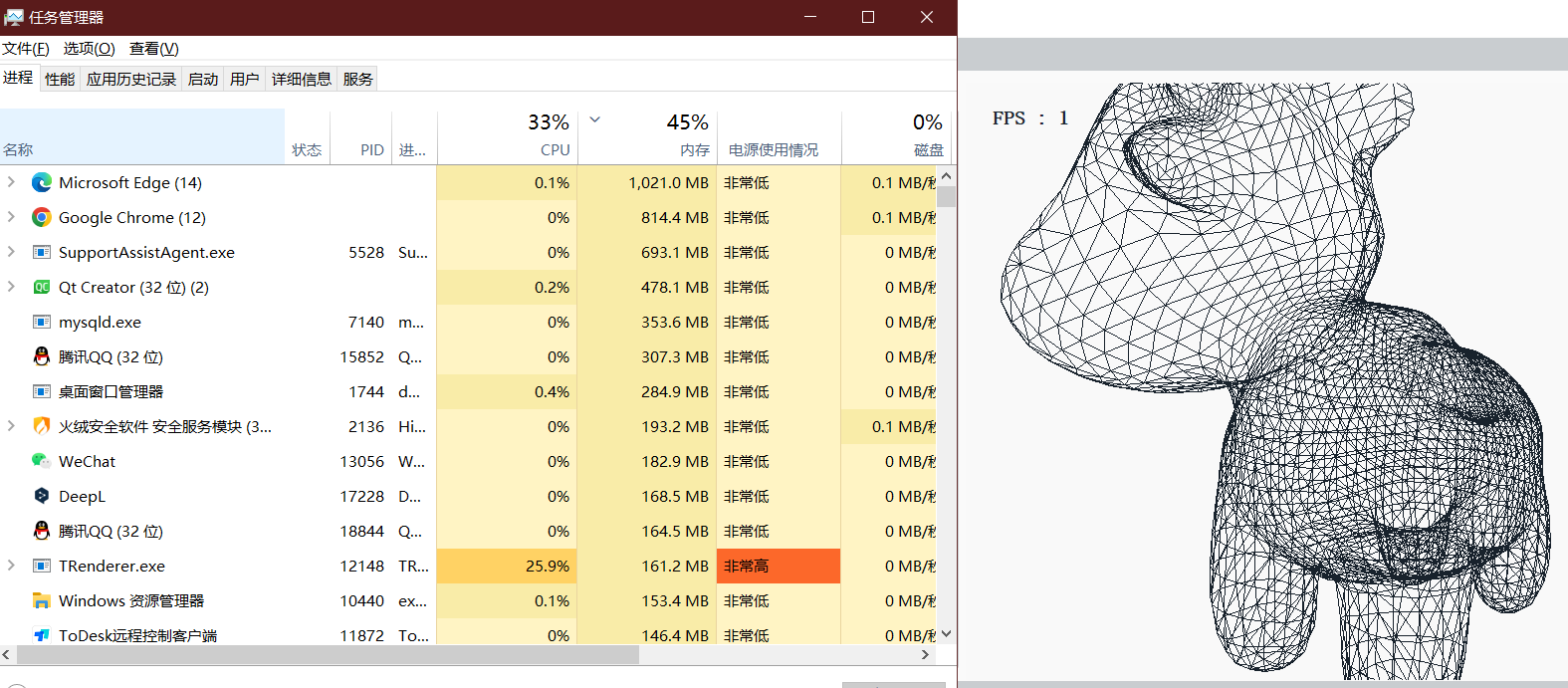
帧率更低了...
应该是线程开的太多
换成16线程
std::vector<std::thread> threads;
size_t numThreads = 16; // 要开启的线程数量
// 计算每个线程处理的元素数量
size_t elementsPerThread = triangleList.size() / numThreads;
size_t remainder = triangleList.size() % numThreads;
// 创建线程
size_t startIdx = 0;
for (size_t i = 0; i < numThreads; ++i) {
size_t threadElements = elementsPerThread + (i < remainder ? 1 : 0);
threads.emplace_back([&](size_t start, size_t end) {
for (size_t idx = start; idx < end; ++idx) {
ProcessTriangle(triangleList[idx]);
}
}, startIdx, startIdx + threadElements);
startIdx += threadElements;
}
// 等待线程执行完毕
for (auto& thread : threads) {
thread.join();
}
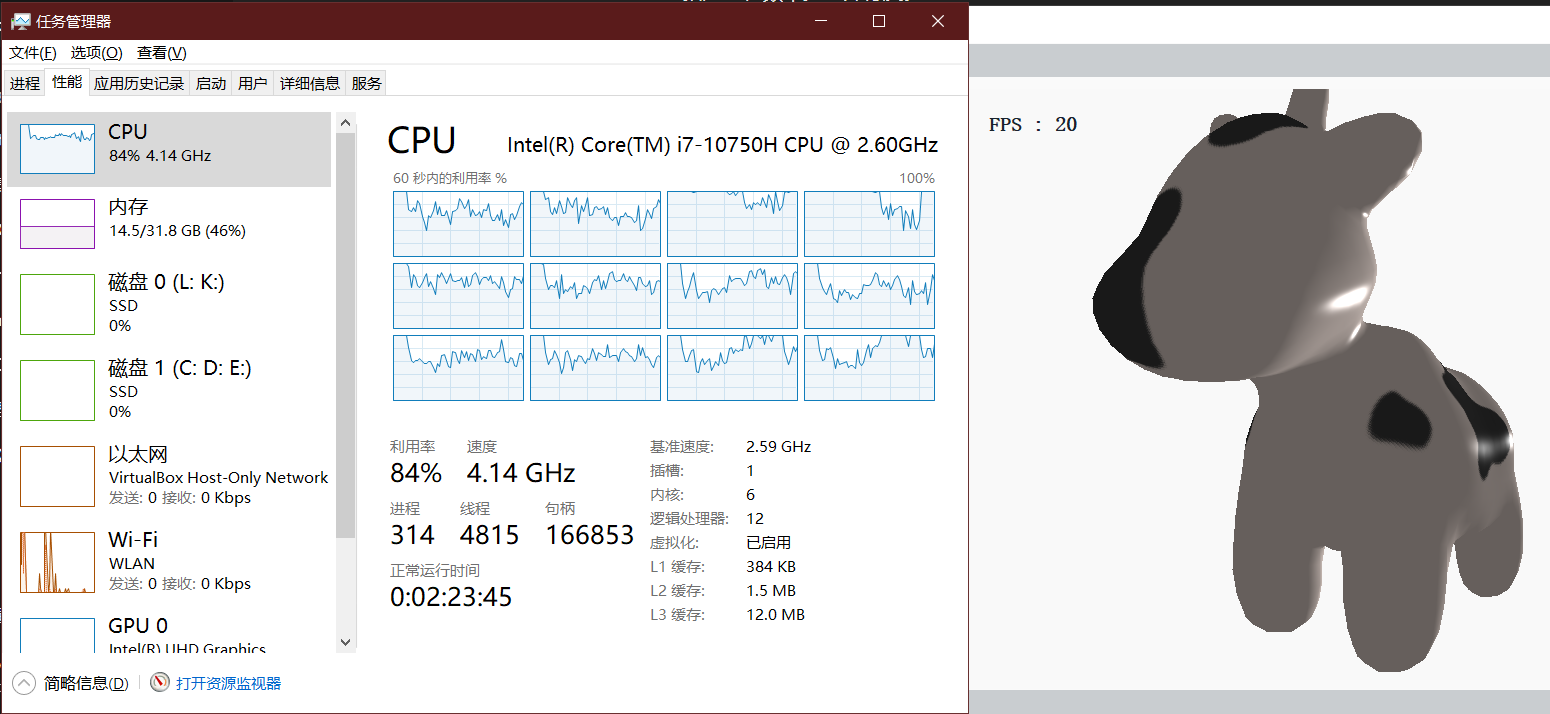
使用后
我又测试了一下开12线程(我的CPU有12核),发现CPU占用
OpenMP
OpenMP 在大多数平台上都有良好的支持,而 std::thread 则依赖于 C++11 标准库和编译器的实现,需要确保平台和编译器的兼容性
CMakeLists.txt
#pragma omp parallel for
for(size_t i = 0; i < triangleList.size(); ++i){
ProcessTriangle(triangleList[i]);
}
目前和thread达到的效果区别不大, 有待测试
图形学知识点回顾
渲染管线
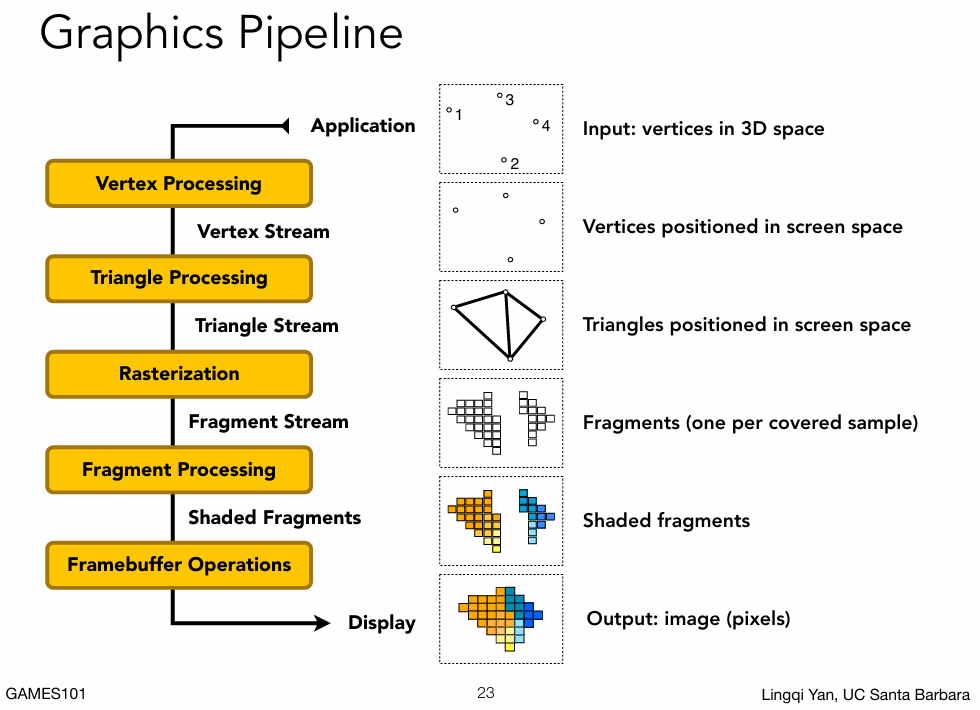
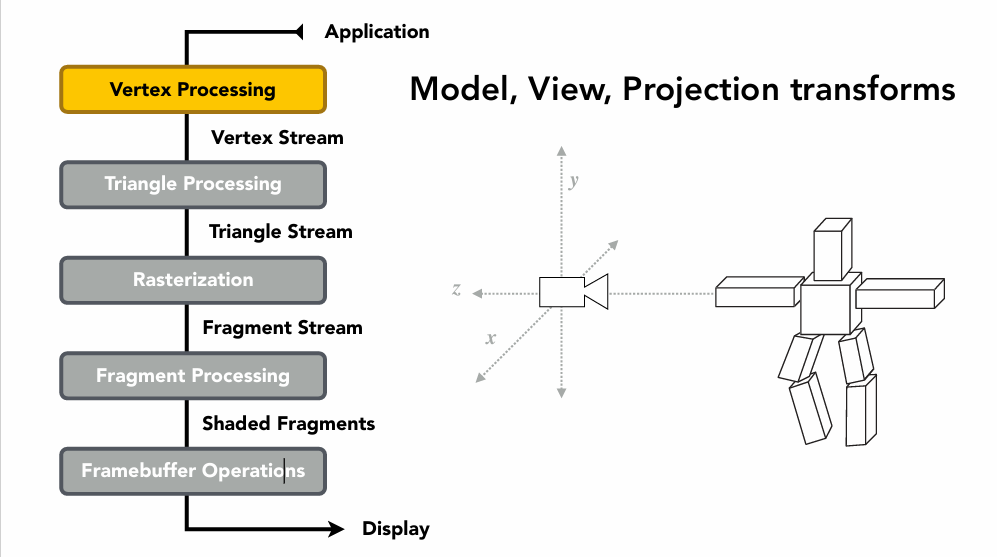
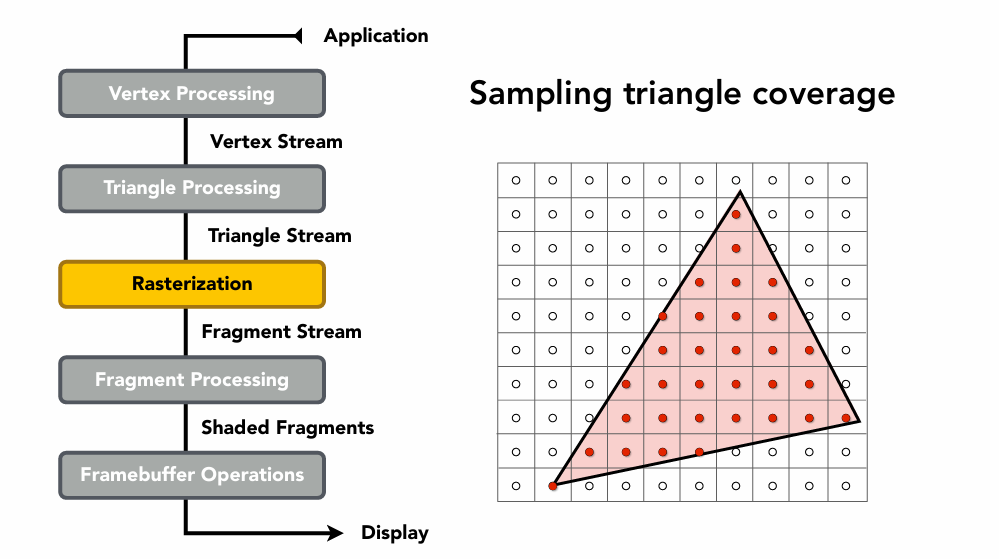
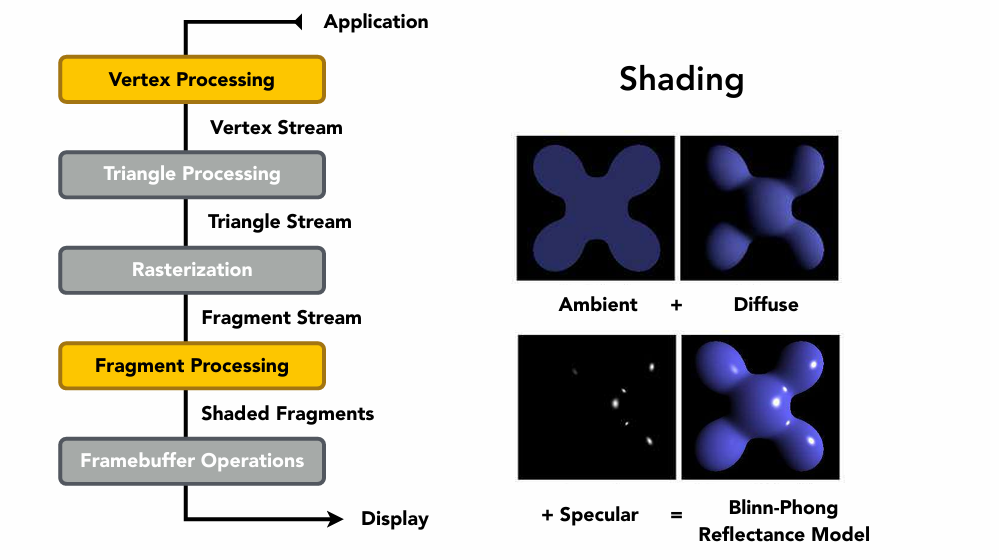
cpp
Mesh() = default;有什么作用
在C++中,Mesh() = default;是一个使用默认构造函数的声明。当您使用Mesh()这种形式声明构造函数时,编译器会生成一个默认构造函数,该构造函数会对类的成员变量进行初始化。如果没有显式声明构造函数,编译器会为类生成一个默认构造函数,这个默认构造函数会对类的基本数据类型进行零初始化(例如,整型数据会初始化为0,浮点型数据会初始化为0.0)。
使用Mesh() = default;的声明方式,您在某种程度上告诉编译器:使用默认的构造函数,而不需要您自己手动实现构造函数。这样可以简化代码,尤其是对于没有特殊构造逻辑的类。
some tips
Vector4D 和 VectorI4D
Vector4D 和 VectorI4D 都表示四维向量,但它们的数据类型有所不同:
- Vector4D:
Vector4D通常指的是四维浮点数向量,即四个浮点数组成的向量。在图形学和计算机图形领域中,常用的表示方法是使用浮点数表示向量的坐标分量。-
例如,一个
Vector4D可以表示为(x, y, z, w),其中x,y,z是浮点数坐标,w通常用于表示齐次坐标中的缩放因子。 -
VectorI4D:
VectorI4D则表示四维整数向量,即四个整数组成的向量。在某些需要使用整数表示坐标或其他数据的情况下,可以使用整数向量。- 例如,一个
VectorI4D可以表示为(x, y, z, w),其中x,y,z是整数坐标,w可以用于其他整数数据。
Vector4D 和 VectorI4D 在表示的数据类型上有所不同,一个是浮点数向量,另一个是整数向量,适用于不同的数据处理场景。
缩放因子w
缩放因子可以在多个场合下使用,如几何变换、透视投影、齐次坐标处理以及光照计算等方面,用来调整物体的大小、深度、权重或者其他影响因素。
-
齐次坐标:在三维图形学中,齐次坐标是一种扩展的坐标系统,其中每个点由四个坐标表示(x, y, z, w)。w 是齐次坐标的缩放因子,用来
表示点的权重或深度信息。通过齐次坐标,可以简化对坐标变换的处理,例如平移、旋转和缩放。 -
透视投影:进行透视投影时,缩放因子可以用来
控制远近平面的拉伸效果。在透视投影中,距离摄像机远的物体会被拉伸,而缩放因子可以影响这种拉伸的程度。 -
几何变换:在进行几何变换(例如缩放、旋转、平移)时,缩放因子可以用来
控制物体的大小变化。通过调整缩放因子,可以实现物体的放大或缩小效果。 -
光照计算:在光照计算中,缩放因子可以
影响光照效果的强度。例如,在 Phong 光照模型中,光照强度与法向量和光线方向的夹角以及缩放因子等因素相关。
俯仰角(pitch)和偏航角(yaw)
- 俯仰角(Pitch):俯仰角是指相对于参考平面(通常是水平面)的上下旋转角度。当俯仰角为正时,物体或相机向上旋转;当俯仰角为负时,物体或相机向下旋转。在图形学中,俯仰角常用来调整相机的仰角,从而改变观察者的视角。
- 偏航角(Yaw):偏航角是指相对于参考方向(通常是水平方向)的左右旋转角度。当偏航角为正时,物体或相机向左旋转;当偏航角为负时,物体或相机向右旋转。在图形学中,偏航角常用来调整相机的水平旋转角度,从而改变观察者的水平方向。
DEBUG(⛔:未解决 / 🌈:已解决)
🌈[error]: CMakeFiles/.../TRendererDevice.cpp.obj: in function `Shader::~Shader()':
error: CMakeFiles/TRenderer.dir/TRendererCore/TRendererDevice.cpp.obj: in function `Shader::~Shader()':
K:\code\QTProject\TRenderer\TRendererCore\Shader.hpp:13: error: undefined reference to `__imp__ZTV6Shader'
声明了一个析构函数 ~Shader(), 但是没有提供对应的定义
需要在实现文件( Shader.cpp)中提供对析构函数 ~Shader() 的定义。例如:
而本项目中Shader 类是一个纯虚基类, 则需要为析构函数提供一个纯虚函数定义。
将析构函数定义为纯虚函数:
然后可在派生类中实现该纯虚析构函数。
附:Shader 类在 TRendererDevice 类中的作用
Shader 类在 TRendererDevice 类中的作用是定义了一个抽象的着色器接口,
从而允许用户根据需要实现不同的着色器类来定制渲染效果。
在
TRendererDevice.h中,Shader类起到了定义一个抽象基类的作用。这个抽象基类是一个纯虚类, 它定义了一些虚函数VertexShader和FragmentShader, 这些函数需要派生类来实现。这样做的目的是
为了实现着色器的多态性, 允许用户根据需要创建不同的着色器类(如顶点着色器、片元着色器)并实现这些虚函数, 以达到不同的渲染效果。具体来说,
Shader类的定义在Shader.hpp文件中, 包含了以下成员函数声明:在
TRendererDevice类中, 有一个指向Shader类或其派生类对象的智能指针:通过这个成员变量,
TRendererDevice类可以在渲染过程中使用用户指定的着色器来处理顶点和片元的着色逻辑。在
TRendererDevice类的渲染过程中, 可能会调用Shader类中定义的虚函数, 例如上面的VertexShader和FragmentShader这些函数会在派生类中被实现, 从而实现具体的顶点和片元着色逻辑。